Advancing Density Functional Tight-Binding for Large Organic Molecules through Equivariant Neural Networks

Introduction

Computers can predict how molecules behave by solving quantum-mechanical equations. Unfortunately, the most accurate approaches, such as density functional theory (DFT), are far too slow for large or complex systems. This is where Density Functional Tight-Binding (DFTB) comes in: a faster and simpler semi-empirical method that approximates these equations. However, DFTB can miss important details, especially when molecules are large enough for electrostatics and polarization effects to play a key role.

In Advancing Density Functional Tight-Binding for Large Organic Molecules through Equivariant Neural Networks, Leonardo Medrano Sandonas, Mirela Puleva, Ricardo Parra, Gianaurelio Cuniberti, and Alexandre Tkatchenko tackle this classic computational chemistry dilemma: choosing between fast methods that sacrifice detail and highly accurate methods that demand heavy computation. By integrating a physics-aware neural network into the DFTB framework, they achieve DFT-PBE0 level precision in property calculations for systems ranging from small dimers to large drug-like molecules, at only twice the usual computational cost of standard DFTB.

The Challenge of This Research

Semi-empirical methods such as DFTB accelerate quantum-mechanical calculations by simplifying how atoms interact, but they struggle with complex and flexible (bio)molecules. Purely machine-learned (ML) potentials can capture such effects for familiar chemistries, yet often falter when applied to larger or previously unseen molecules. Crucially, any correction must still respect the laws of physics, producing identical results when the molecule is rotated or translated in space.

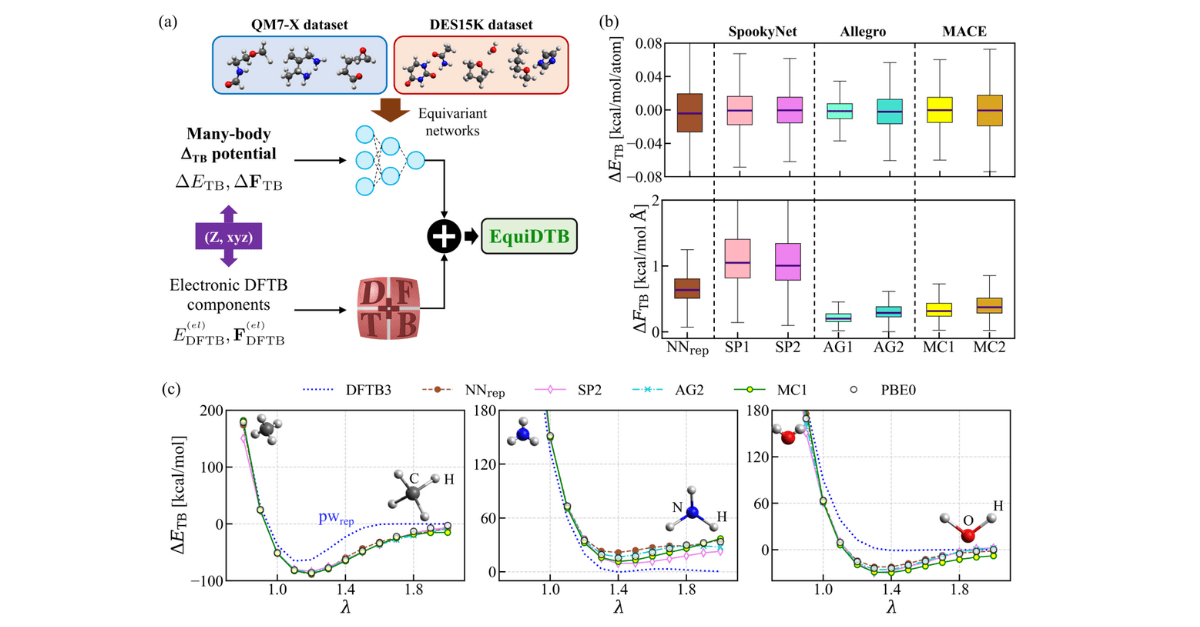
The EquiDTB Solution

Hybrid quantum-ML model

The team kept DFTB3’s electronic backbone and added a ΔTB correction from an SE(3)-equivariant neural network to achieve DFT-PBE0 accuracy. This design ensures predictions remain consistent under any rotation or translation.

Comparing equivariant architectures

Three leading network designs; SpookyNet, Allegro and MACE, were trained on benchmark datasets for small molecules and non-bonded pairs, learning to reproduce high-level reference energies and forces.

Dispersion for long-range effects

A many-body dispersion term captures subtle van der Waals forces, so interactions between distant atoms are described adequately.

*Schematic of the EquiDTB workflow, showing how DFTB3’s electronic energy and forces combine with the ΔTB many-body correction from an SE(3)-equivariant neural network.*

MeluXina’s Contribution

Training and benchmarking these complex hybrid QM/ML models required substantial computational resources, which is where the MeluXina supercomputer came into play. All major model training runs, architecture comparisons, and large-scale validation tasks were executed on MeluXina. The supercomputer’s GPU-accelerated nodes enabled rapid experimentation with multiple network designs and large molecular databases, reducing computation time from weeks to days. This acceleration made it possible to refine the approach across a wide range of molecular systems in a fraction of the usual time.

The Impact

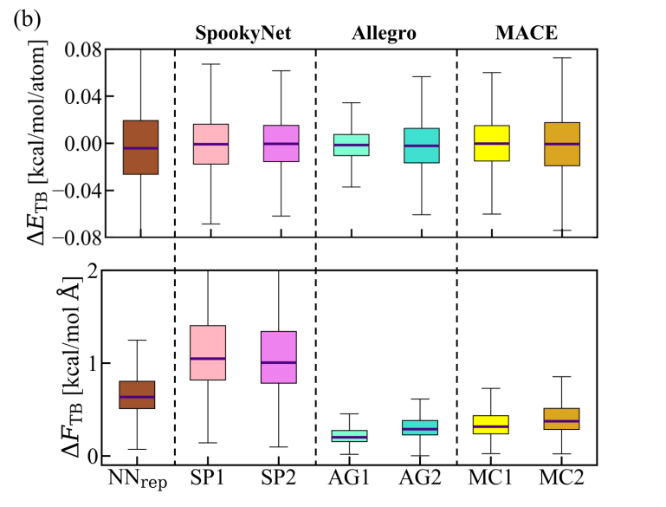
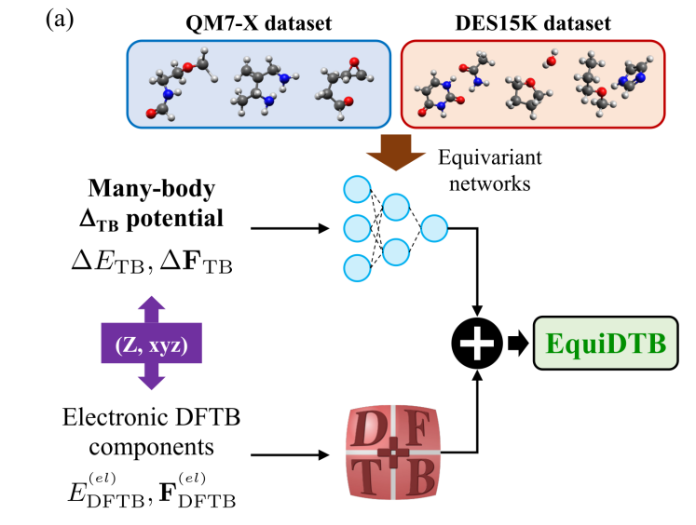
(a) Boxplots of energy (ΔETB) and force (ΔFTB) errors on QM7-X molecules for three equivariant architectures (SpookyNet, Allegro, MACE) versus the earlier NNrep model. Validation of EquiDTB model for computing (b) rotational energy profiles and (c) vibrational frequencies of unseen and large molcules.

Near hybrid-DFT precision

Energy errors drop to ~0.02 kcal mol⁻¹ per atom and force errors to ~0.3 kcal mol⁻¹ Å⁻¹.

Reliable modelling of non-covalent systems

On the S66x8 dimer test, binding energy errors stay under 1 kcal mol⁻¹, while force errors achieves ~0.5 kcal mol⁻¹ Å⁻¹.

Transferable to large and unseen molecules

Predicts energy barriers within 0.5 kcal mol⁻¹ and ranks conformers of large durg-like compounds almost as accurately as top-tier methods. Amino-acid vibrational frequencies match reference within ~5 cm⁻¹.

More accurate than pure ML potentials

The EquiDTB model outperforms an ML potential trained on absolute energies and forces across several benchmarks.

Conclusion

EquiDTB shows that combining DFTB with an equivariant neural network and dispersion corrections can achieve DFT-level accuracy for a wide range of molecular systems at a fraction of the computational cost. Thanks to MeluXina’s GPU-accelerated resources, this approach scales to sizeable and flexible molecular systems, offering a practical path for high-fidelity simulations in drug development, materials science and beyond.

<< back